Digital Audio Sampling 2

Returning to our sine wave, this tutorial will focus a bit more on those positive and negative fluctuations in air pressure. Recall that the waveform was centered around a zero line that represented silence.

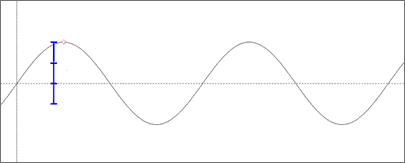
How far the waveform deviates from this center line is dependent on how loud the sound is. This is referred to as the sound's amplitude. If the amplitude is smaller, like this...

...it will be quieter than the first example. When comparing these two examples, you should notice that nothing else about the waveform has changed. The frequency of the sine wave has remained constant and the "pitch" will therefore not change. It is simply the "loudness" that has been affected.

In order to record these changes in amplitude digitally, a specific amount of memory must be allocated for each sample. How much memory is a factor in how closely the digital recording can match changes in the original. This is called bit depth and it is measured by the number of bits allocated for each digital sample. Greater bit depth means more accuracy because it allows for a greater number of different values to be recorded, but it also means more memory and larger file sizes.

If we were to use a bit depth of 1, we would only have two options for our amplitude...

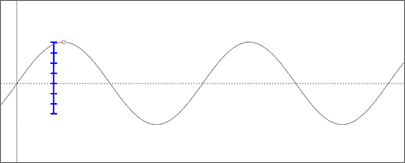
This will obviously not be sufficient. Using two bits is not much better, providing only four different values to be recorded...

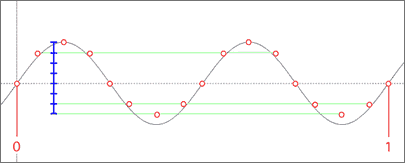
Notice that we lose one value in a sense, because it must be reserved for the center line. At three bits, we would have eight possible values and would be able to have a much better start for our example...

So if we were to sample this waveform at 16 Hz, we would capture enough of the changes in time to recreate it without the frequency aliasing...

But if only 3 bits were used to recorded each amplitude value, these samples would have to lock into one of the 8 values available...

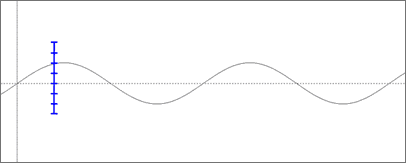
These errors result from the limitations of a digital audio system. At lower bit depths, the errors are so great that they lead to what is called quantization noise.

Problems can also result from the sounds being recorded at a low volume. If we were to again lower the amplitude on our sine wave...

You can see that less of the available dynamic range is being used. The dynamic range that is "possible" is fixed by the bit depth. Recording sounds a too low a volume will cause them to be more prone to quantization noise, because they are effectively using fewer digital values than if they were at full volume.

CDs operate at a bit depth of 16, meaning they are capable of 65,536 different values. Each bit of digital sampling provides approximately 6 dB of dynamic range. Using this information we can conclude...

16 bits * 6 dB = 96 dB

96 decibels is a large range, but not quit as much as our ears are can hear (we have about 120 dB of hearing range). But for the majority of purposes, it will do.

Although all these numbers seem very abstract, remember this is how your computer is dealing with sound. It is important to have some understanding of how this works so that you can have a better understanding of what the computer must do in order for you to hear sounds. Inevitably, problems caused by limitations in this system will occur and you must be able to identify them as such, without assigning blame on the computer or the program developer.